前置技能

平衡树是二叉搜索树的一种，二叉搜索树的定义如下：

  • 空树是二叉搜索树
  • 若二叉搜索树的左子树不为空，则其左子树上所有点的权值均小于其根节点的值
  • 若二叉搜索树的右子树不为空，则其右子树上所有点的权值均大于其根节点的值
  • 二叉搜索树的左右子树均为二叉搜索树

对于有$n$个节点的二叉搜索树，每次基本操作的最优复杂度为$O(logn)$，由于二叉搜索树可能退化成一条链，所以最坏复杂度$O(n)$

而每种平衡树都能通过一些方法让二叉搜索树不退化成一条链，每次操作的时间复杂度保持在$O(logn)$

平衡树主要分为两种：

  • 有旋转的树：AVL树，Splay树，红黑树
  • 无旋转的树：替罪羊树，fhq-Treap

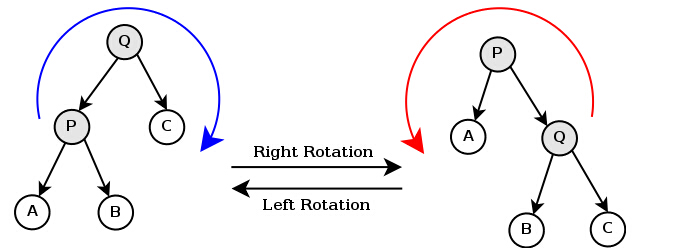
树旋转也分为两种：

  • 右旋：将自己变为左孩子的右孩子，同时将左孩子的右孩子变为自己的左孩子
  • 左旋：将自己变为右孩子的左孩子，同时将右孩子的左孩子变为自己的右孩子

替罪羊树

替罪羊树通过重构来维持树的平衡，在插入、删除操作之后，从上到下检测途经的节点，若发现失衡，则将以该节点为根的子树重构

1
2
3
4
5
6
7
struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int sz;     // 包括已删除节点的子树大小
    int fsz;    // 实际大小，不包括已删除节点的子树大小
    int cnt;    // 数据出现的次数
};

替罪羊树的删除是一种惰性删除，只是打上一个标记表示该节点已经被删除，实际大小就是没有被打上标记的节点数量，这个标记就是cnt，cnt=0表示节点已经被删除，cnt>0是表示节点存在

为了判断节点是否需要重构，我们定义一个平衡因子$\alpha$(取值在0.5到1之间)，一般取0.75，当满足以下两个条件时表示该节点需要重构

  • 左子树或者右子树的sz大于整个子树的sz * $\alpha$(左子树或者右子树太大导致整个子树不平衡)
  • 整个子树被删除的节点数量大于整个子树的sz * 0.3(被删除的节点太多导致整个子树不平衡)
1
2
3
4
5
6
bool imbalance(int &now)
{
    if (max(tree[tree[now].l].sz, tree[tree[now].r].sz) > tree[now].sz * alpha) return true;
    if (tree[now].sz - tree[now].fsz > tree[now].sz * 0.3) return true;
    return false;
}

对于需要重构的节点，重构分为两步：

  • 先中序遍历展开存入向量，注意只有当前节点存在时(cnt>0)才能够存入向量
  • 分治建二叉树(每次取区间中点作为根，然后递归两边为左右子树建树)

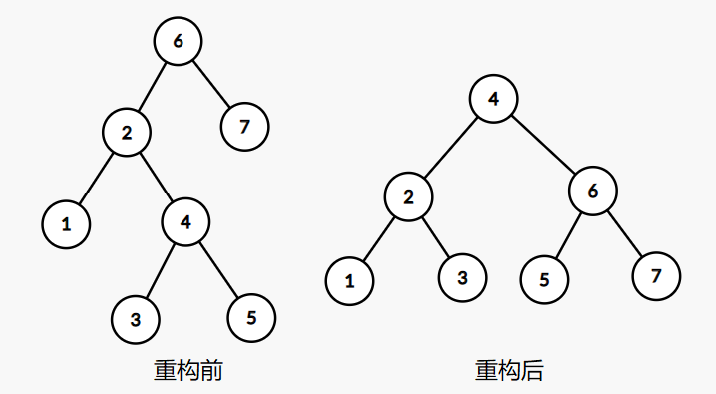
在分治的同时，更新重构后子树每个节点的sz和fsz

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void dfs(int &now)
{
    if (0 == now) return;
    dfs(tree[now].l);
    if (tree[now].cnt) v.push_back(now);
    dfs(tree[now].r);
}

void lift(int l, int r, int &now)
{
    if (l == r) {
        now = v[l];
        tree[now].l = tree[now].r = 0;
        tree[now].sz = tree[now].fsz = tree[now].cnt;
        return;
    }
    int mid = (l + r) / 2;
    now = v[mid];
    if (l < mid) lift(l, mid - 1, tree[now].l);
    else tree[now].l = 0;
    lift(mid + 1, r, tree[now].r);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void rebuild(int &now)
{
    v.clear();
    dfs(now);
    if (v.empty()) {
        now = 0;
        return;
    }
    lift(0, (int)v.size() - 1, now);
}

显然，对一颗重构后的子树，我们还需要从上向下采用头递归的方式(比较好写，自下而上需要多一个fa参数)更新路径上所有节点的sz和fsz
check函数表示检查now到end路径上所有的点，如果有不平衡的节点则重构以该节点为根的子树
注意：check函数是自上向下检查每个节点是否需要重构，因为如果自下而上判断，可能会导致重构很多次，复杂度不能保证，而自上向下判断只需要重构第一个不平衡的节点即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void update(int &now, int end)
{
    if (now == end) return;
    if (tree[end].val < tree[now].val) update(tree[now].l, end);
    else update(tree[now].r, end);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void check(int &now, int end)
{
    if (now == end) return;
    if (imbalance(now)) {
        rebuild(now);
        update(root, now);
        return;
    }
    if (tree[end].val < tree[now].val) check(tree[now].l, end);
    else check(tree[now].r, end);
}

替罪羊的插入操作和普通二叉搜索树的插入操作差不多，只是在每次插入之后，都需要从根节点root到当前节点now自上向下判断每个节点是否需要重构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void insert(int &now, int val)
{
    if (0 == now) {
        newnode(now, val);
        check(root, now);
        return;
    }
    tree[now].sz++;
    tree[now].fsz++;
    if (val < tree[now].val) insert(tree[now].l, val);
    else if (val == tree[now].val) {
        tree[now].cnt++;
        check(root, now);
    }
    else insert(tree[now].r, val);
}

删除操作同理，每次删除后，从根节点root到当前节点now自上向下判断每个节点是否需要重构

注意：删除操作减少的是节点的fsz，不是节点sz，fsz表示的是真实的大小(不包括已经删除的节点)

1
2
3
4
5
6
7
8
9
10
11
12
void del(int &now, int val)
{
    if (tree[now].cnt && tree[now].val == val) {
        tree[now].cnt--;
        tree[now].fsz--;
        check(root, now);
        return;
    }
    tree[now].fsz--;
    if (val < tree[now].val) del(tree[now].l, val);
    else del(tree[now].r, val);
}

对于查询某个数的排名qrank(x)和查询某个排名上的数qnum(x)，则可以利用二叉搜索树的性质来求解

对于某个数的前驱，只需要查询qnum(qrank(x)-1)，即查询(这个数的排名-1)上的数

但对于后继，不能查询qnum(qrank(x)+1)，因为可能有重复的数字，比如说1 2 2 4，查询2的后继时，2的排名为2，但4的排名却是4，这样查询的结果依然是2，所以我们应该查询qnum(qrank(x+1))

例题：bzoj-3224普通平衡树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>

using namespace std;

const int N = 100010;
const double alpha = 0.75;

struct node {
    int l, r, val;
    int sz, fsz, cnt;
};

node tree[N];
int root, cnt, n;
vector<int> v;

inline void newnode(int &now, int val)
{
    now = ++cnt;
    tree[now].val = val;
    tree[now].sz = tree[now].fsz = 1;
    tree[now].cnt = 1;
}

bool imbalance(int &now)
{
    if (max(tree[tree[now].l].sz, tree[tree[now].r].sz) > tree[now].sz * alpha) return true;
    if (tree[now].sz - tree[now].fsz > tree[now].sz * 0.3) return true;
    return false;
}

void dfs(int &now)
{
    if (0 == now) return;
    dfs(tree[now].l);
    if (tree[now].cnt) v.push_back(now);
    dfs(tree[now].r);
}

void lift(int l, int r, int &now)
{
    if (l == r) {
        now = v[l];
        tree[now].l = tree[now].r = 0;
        tree[now].sz = tree[now].fsz = tree[now].cnt;
        return;
    }
    int mid = (l + r) / 2;
    now = v[mid];
    if (l < mid) lift(l, mid - 1, tree[now].l);
    else tree[now].l = 0;
    lift(mid + 1, r, tree[now].r);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void rebuild(int &now)
{
    v.clear();
    dfs(now);
    if (v.empty()) {
        now = 0;
        return;
    }
    lift(0, (int)v.size() - 1, now);
}

void update(int &now, int end)
{
    if (now == end) return;
    if (tree[end].val < tree[now].val) update(tree[now].l, end);
    else update(tree[now].r, end);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void check(int &now, int end)
{
    if (now == end) return;
    if (imbalance(now)) {
        rebuild(now);
        update(root, now);
        return;
    }
    if (tree[end].val < tree[now].val) check(tree[now].l, end);
    else check(tree[now].r, end);
}

void insert(int &now, int val)
{
    if (0 == now) {
        newnode(now, val);
        check(root, now);
        return;
    }
    tree[now].sz++;
    tree[now].fsz++;
    if (val < tree[now].val) insert(tree[now].l, val);
    else if (val == tree[now].val) {
        tree[now].cnt++;
        check(root, now);
    }
    else insert(tree[now].r, val);
}

void del(int &now, int val)
{
    if (tree[now].cnt && tree[now].val == val) {
        tree[now].cnt--;
        tree[now].fsz--;
        check(root, now);
        return;
    }
    tree[now].fsz--;
    if (val < tree[now].val) del(tree[now].l, val);
    else del(tree[now].r, val);
}

int qrank(int val)
{
    int now = root, rank = 1;
    while (now) {
        if (val <= tree[now].val) now = tree[now].l;
        else {
            rank = rank + tree[tree[now].l].fsz + tree[now].cnt;
            now = tree[now].r;
        }
    }
    return rank;
}

int qnum(int rank)
{
    int now = root;
    while (now) {
        int lz = tree[tree[now].l].fsz;
        if (tree[now].cnt && rank >= lz + 1 && rank <= lz + tree[now].cnt) break;
        if (lz >= rank) now = tree[now].l;
        else {
            rank = rank - lz - tree[now].cnt;
            now = tree[now].r;
        }
    }
    return tree[now].val;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int op, x;
        scanf("%d%d", &op, &x);
        if (1 == op) insert(root, x);
        else if (2 == op) del(root, x);
        else if (3 == op) printf("%d\n", qrank(x));
        else if (4 == op) printf("%d\n", qnum(x));
        else if (5 == op) printf("%d\n", qnum(qrank(x) - 1));
        else printf("%d\n", qnum(qrank(x + 1)));
    }
    return 0;
}

fhq-Treap

treap是单词tree和heap的组合，表明treap是一种由树和堆组成的数据结构，所以fhq-Treap的每个节点都必须存储val和key两个值，其中val表示节点权值，key是随机的一个值，val满足二叉搜索树的性质，而key满足堆的性质，由于key是随机的，所以treap是期望平衡的

1
2
3
4
5
6
struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int key;    // 随机的关键值
    int sz;     // 以该节点为根的子树大小
};

fhq-Treap只有两个基本操作：分裂split和合并merge

分裂分为两种：

  • 按值val分裂：把树分裂成两棵树，其中一棵树上所有节点的权值都小于等于val，另一颗树上所有节点的权值都大于val
  • 按大小分裂：把树分裂成两棵树，其中一棵树的大小等于给定的大小，其余的节点在另一棵树里

接下来我们以按值分裂为例，假设权值小于等于val的那一棵树的根节点为x，称为第一棵树，另一棵树的根节点为y，称为第二棵树

根据二叉搜索树的性质，如果当前节点now的权值小于等于val，那么当前节点now和now的左子树都属于第一棵树，然而now的右子树上的节点不一定都属于第一棵树，那么我们就继续递归分裂now的右子树，同理，如果当前节点now的权值大于val，那么当前节点now和now的右子树都属于第二棵树，然而now的左子树上的节点不一定都属于第二棵树，继续递归分裂now的左子树

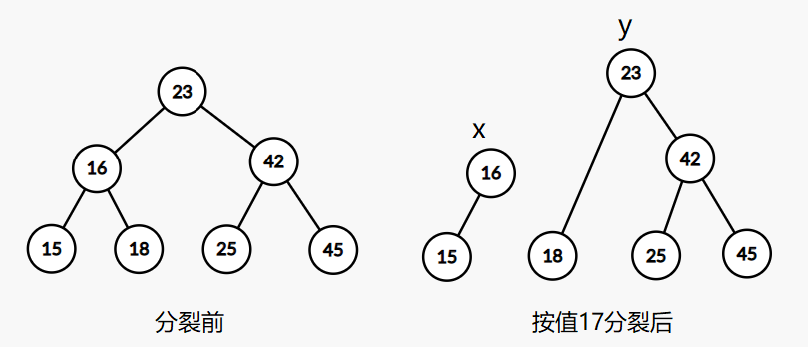
注意：分裂的同时需要更新路径上节点的sz，x和y采用引用传递(比较好写)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
inline void update(int now)
{
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + 1;
}

void split(int now, int val, int &x, int &y)
{
    if (0 == now) {
        x = y = 0;
        return;
    }
    if (tree[now].val <= val) {
        x = now;
        split(tree[now].r, val, tree[now].r, y);
    }
    else {
        y = now;
        split(tree[now].l, val, x, tree[now].l);
    }
    update(now);
}

合并时，以维护小根堆为例，有两种情况：

  • 第一棵树根节点x的key值比第二棵树根节点y的key值小，由于第一棵树上节点的权值都小于第二棵树上节点的权值，那么根据二叉搜索树和小根堆的性质，第一棵树就在第二棵树的“左上方”，此时就递归合并节点x的右子树和节点y
  • 第二棵树根节点x的key值比第二棵树根节点y的key值大，同理，那么第一棵树就在第二棵树的“左下方”，此时递归合并节点x和节点y的左子树

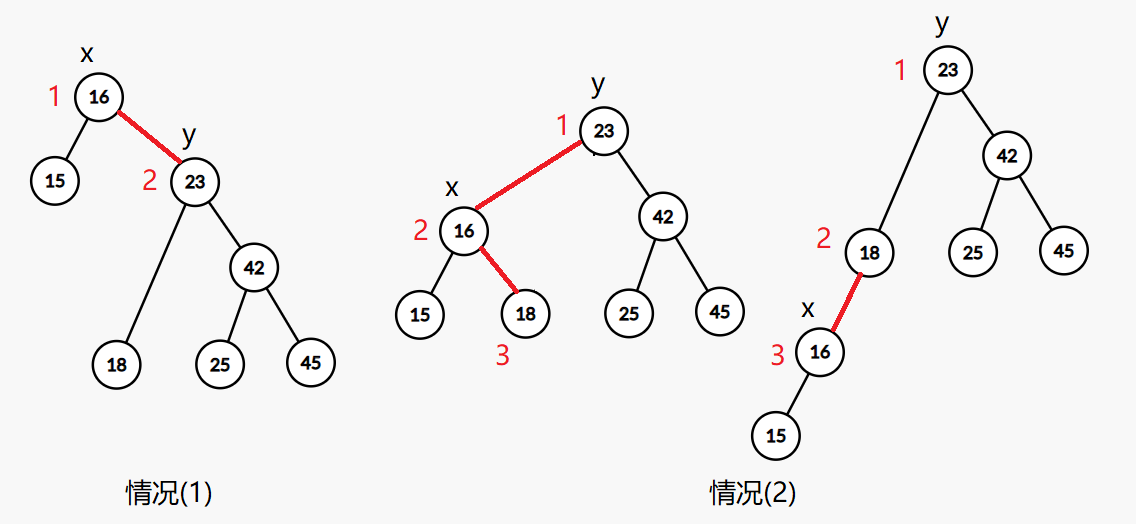
merge(x,y)表示将以x为根的树和以y为根的树合并同时返回合并后的根节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

有了分裂split和合并merge操作之后，二叉搜索树的基本操作就能用这两个操作来表示出来，以插入操作为例，假设需要插入节点的值为val，我们先可以将树按val分裂成两棵树，再将第一棵树，新节点，第二棵树按照顺序依次合并成一棵树

1
2
3
4
5
6
inline void insert(int val)
{
    int x, y;
    split(root, val, x, y);
    root = merge(merge(x, newnode(val)), y);
}

例题：bzoj-3224普通平衡树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <stdlib.h>

using namespace std;

const int N = 100010;
const int M = 1000;

struct node {
    int l, r;
    int val, key, sz;
};

node tree[N];
int cnt, root, t;

inline int newnode(int val)
{
    tree[++cnt].val = val;
    tree[cnt].key = rand() % M;
    tree[cnt].sz = 1;
    return cnt;
}

inline void update(int now)
{
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + 1;
}

void split(int now, int val, int &x, int &y)
{
    if (0 == now) {
        x = y = 0;
        return;
    }
    if (tree[now].val <= val) {
        x = now;
        split(tree[now].r, val, tree[now].r, y);
    }
    else {
        y = now;
        split(tree[now].l, val, x, tree[now].l);
    }
    update(now);
}

int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

inline void insert(int val)
{
    int x, y;
    split(root, val, x, y);
    root = merge(merge(x, newnode(val)), y);
}

inline void del(int val)
{
    int x, y, z;
    split(root, val, x, z);
    split(x, val - 1, x, y);
    y = merge(tree[y].l, tree[y].r);
    root = merge(merge(x, y), z);
}

inline int qr(int val)
{
    int x, y;
    split(root, val - 1, x, y);
    int res = tree[x].sz + 1;
    root = merge(x, y);
    return res;
}

inline int qn(int rank)
{
    int now = root;
    while (now) {
        if (tree[tree[now].l].sz + 1 == rank) break;
        else if (tree[tree[now].l].sz >= rank)
            now = tree[now].l;
        else {
            rank = rank - tree[tree[now].l].sz - 1;
            now = tree[now].r;
        }
    }
    return tree[now].val;
}

inline int pre(int val)
{
    int x, y;
    split(root, val - 1, x, y);
    int now = x;
    while (tree[now].r) now = tree[now].r;
    int res = tree[now].val;
    root = merge(x, y);
    return res;
}

inline int nex(int val)
{
    int x, y;
    split(root, val, x, y);
    int now = y;
    while (tree[now].l) now = tree[now].l;
    int res = tree[now].val;
    root = merge(x, y);
    return res;
}

int main()
{
    scanf("%d", &t);
    while (t--) {
        int opt, x;
        scanf("%d%d", &opt, &x);
        if (1 == opt) insert(x);
        if (2 == opt) del(x);
        if (3 == opt) printf("%d\n", qr(x));
        if (4 == opt) printf("%d\n", qn(x));
        if (5 == opt) printf("%d\n", pre(x));
        if (6 == opt) printf("%d\n", nex(x));
    }
    return 0;
}

fhq-Treap还可以对区间信息进行维护，包括区间反转，区间交换等等，这时就需要按大小进行分裂，fhq-Treap对区间[l,r]操作的核心思想仍然是分裂，将区间[l,r]直接从树中分裂出来

fhq-Treap对区间的操作和线段树类似，需要维护一个懒标记，当进行分裂和合并时需要下传懒标记

此时fhq-Treap仍然用随机的关键值key维护堆的性质，但不再用节点的权值维护二叉树的性质，而是用该点在序列中的位置来维护二叉树的性质，显然对这棵树中序遍历一遍就可以得到原序列

注意：这个“该点在序列中的位置”并不会体现在代码中，在分裂时而是通过当前节点now左子树的大小与需要分裂的大小sz的大小关系来决定是向左子树移动还是向右子树移动

分裂时，如果当前节点now左子树的大小小于还需要分裂的大小sz，那么当前节点now和now的左子树都应该属于第一棵树，同时递归分裂now的右子树，此时还需要分裂的大小sz应该减去刚刚分裂出的树的大小(now左子树的大小+1)，同理，如果前节点now左子树的大小大于等于还需要分裂的大小sz，则应该递归分裂now的左子树

由于这棵树是按该点在序列中的位置来维护二叉树性质的，所以分裂后第一棵树表示的区间就是[1,sz]，其他节点在第二棵树上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void split(int now, int sz, int &x, int &y)
{
    if (0 == now) x = y = 0;
    else {
        pushdown(now);
        if (tree[tree[now].l].sz < sz) {
            x = now;
            split(tree[now].r, sz - tree[tree[now].l].sz - 1, tree[now].r, y);
        }
        else {
            y = now;
            split(tree[now].l, sz, x, tree[now].l);
        }
        update(now);
    }
}

因为仍然使用关键值key维护fhq-Treap堆的性质，所以合并merge和按值分裂只多了把懒标记向下传递的过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        pushdown(x);
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        pushdown(y);
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

有了分裂split和合并merge操作之后，对于区间[l,r]，可以先分裂出[1,r]区间，再将区间[1,r]分裂为[1,l-1]和[l,r]两个区间

例题：poj-3580 SuperMemo

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <stdlib.h>

using namespace std;

const int N = 200010;
const int M = 1000;
const int INF = 0x3f3f3f3f;

struct node {
    int l, r, key, sz, rev;
    int val, imin, lz;
};

node tree[N];
int cnt, root, t, n, m;
char s[M];

void flip(int x)
{
    swap(tree[x].l, tree[x].r);
    tree[tree[x].l].rev ^= 1;
    tree[tree[x].r].rev ^= 1;
    tree[x].rev = 0;
}

void add(int x, int val)
{
    if (0 == x) return;
    tree[x].val += val;
    tree[x].imin += val;
    tree[x].lz += val;
}

void update(int x)
{
    tree[x].sz = tree[tree[x].l].sz + tree[tree[x].r].sz + 1;
    tree[x].imin = min(tree[x].val, min(tree[tree[x].l].imin, tree[tree[x].r].imin));
}

void pushdown(int x)
{
    if (tree[x].rev) flip(x);
    if (tree[x].lz) {
        add(tree[x].l, tree[x].lz);
        add(tree[x].r, tree[x].lz);
        tree[x].lz = 0;
    }
}

int newnode(int val)
{
    tree[++cnt].val = val;
    tree[cnt].imin = val;
    tree[cnt].key = rand() % M;
    tree[cnt].sz = 1;
    return cnt;
}

void split(int now, int sz, int &x, int &y)
{
    if (0 == now) x = y = 0;
    else {
        pushdown(now);
        if (tree[tree[now].l].sz < sz) {
            x = now;
            split(tree[now].r, sz - tree[tree[now].l].sz - 1, tree[now].r, y);
        }
        else {
            y = now;
            split(tree[now].l, sz, x, tree[now].l);
        }
        update(now);
    }
}

int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        pushdown(x);
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        pushdown(y);
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

void insert(int k, int val)
{
    int x, y;
    split(root, k, x, y);
    root = merge(merge(x, newnode(val)), y);
}

void del(int k)
{
    int x, y, z;
    split(root, k - 1, x, y);
    split(y, 1, y, z);
    root = merge(x, z);
}

int qimin(int l, int r)
{
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    int res = tree[y].imin;
    root = merge(x, merge(y, z));
    return res;
}

void qadd(int l, int r, int val)
{
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    add(y, val);
    root = merge(x, merge(y, z));
}

void qreverse(int l, int r)
{
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    tree[y].rev ^= 1;
    root = merge(x, merge(y, z));
}

void qrevolve(int l, int r, int len)
{
    len %= (r - l + 1);
    if (0 == len) return;
    int x, y, z, k;
    split(root, r, x, k);
    split(x, l - 1, x, y);
    split(y, r - l + 1 - len, y, z);
    root = merge(x, merge(merge(z, y), k));
}

int main()
{
    tree[0].val = tree[0].imin = INF;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int val;
        scanf("%d", &val);
        root = merge(root, newnode(val));
    }
    scanf("%d", &m);
    while (m--) {
        scanf("%s", s + 1);
        int l, r, k, val;
        if ('A' == s[1]) {
            scanf("%d%d%d", &l, &r, &val);
            qadd(l, r, val);
        }
        else if ('R' == s[1] && 'E' == s[4]) {
            scanf("%d%d", &l, &r);
            qreverse(l, r);
        }
        else if ('R' == s[1] && 'O' == s[4]) {
            scanf("%d%d%d", &l, &r, &k);
            qrevolve(l, r, k);
        }
        else if ('I' == s[1]) {
            scanf("%d%d", &l, &val);
            insert(l, val);
        }
        else if ('D' == s[1]) {
            scanf("%d", &l);
            del(l);
        }
        else {
            scanf("%d%d", &l, &r);
            printf("%d\n", qimin(l, r));
        }
    }
    return 0;
}

fhq-Treap最大的缺点就是常数很大，有时候会被卡，Splay常数小，不容易被卡

AVL树

AVL树为了维持树的平衡，引入了平衡因子BF的概念，平衡因子=左子树树高-右子树树高(右子树树高-左子树树高)

1
2
3
4
5
6
struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int h;      // 树高
    int sz;     // 以该节点为根的子树大小
};

AVL树中每个节点的平衡因子只能为-1，0或1，当某个节点的平衡因子过大或者过小时，则通过树旋转的方式来让树恢复平衡，显然AVL树的树高为$O(logn)$，每次操作的时间复杂度为$O(logn)$

向一棵平衡的AVL数中插入或者删除一个节点，在没有调整前，树中每个节点平衡因子的取值只能为-2，-1，0，1或2

那么以下四种情况需要调整：

  • LL：在当前节点now左子树的左子树上插入节点导致树不平衡，此时now的BF>1，now左子树的BF>0(插入之前可能为0或者1)，右旋当前节点now使树平衡
  • LR：在当前节点now左子树的右子树上插入节点导致树不平衡，此时now的BF>1，而now右子树的BF<=0(插入之前可能为1，0，-1)，先左旋now的左子树，再右旋当前节点使树平衡
  • RL：在当前节点now右子树的左子树上插入节点导致树不平衡，先右旋now的右子树，再左旋当前节点使树平衡
  • RR：在当前节点now右子树的右子树上插入节点导致树不平衡，左旋当前节点 now使树平衡

旋转之后需要更新当前节点now和now左右子树的大小、树高

zag表示左旋，zig表示右旋，check检查当前节点now是否平衡

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
inline int calc(int now)
{
    return tree[tree[now].l].h - tree[tree[now].r].h;
}

inline void zag(int &now)
{
    int r = tree[now].r;
    tree[now].r = tree[r].l;
    tree[r].l = now;
    now = r;
    update(tree[now].l);
    update(now);
}

inline void zig(int &now)
{
    int l = tree[now].l;
    tree[now].l = tree[l].r;
    tree[l].r = now;
    now = l;
    update(tree[now].r);
    update(now);
}

inline void check(int &now)
{
    int nf = calc(now);
    if (nf > 1) {
        int lf = calc(tree[now].l);
        if (lf > 0) zig(now);
        else {
            zag(tree[now].l);
            zig(now);
        }
    }
    else if (nf < -1) {
        int rf = calc(tree[now].r);
        if (rf < 0) zag(now);
        else {
            zig(tree[now].r);
            zag(now);
        }
    }
    else if (now) update(now);
}

AVL的插入操作和二叉搜索树几乎没有区别，只是在插入后，自下而上回溯检查路径上的节点是否平衡，所以采用头递归的方式插入

对于删除操作，如果需要删除的节点只有一个儿子节点或者没有儿子节点，那么直接删除就可以了，对于有双儿子的节点，AVL树有两种删除方法：

  • 将需要删除的节点旋转到叶子节点，直接删除即可
  • 先找到需要删除节点的后继节点，用后继节点代替自己的位置，由于后继节点一定没有左儿子，所以后继节点直接删除即可

无论哪种方法，同样在删除后，需要自下而上回溯检查路径上的节点是否平衡

查询某个数的排名qrank(x)和查询某个排名上的数qnum(x)和替罪羊树差不多，只是替罪羊树每个节点可能是多个相同的数，而AVL每个节点都只表示一个数

例题：bzoj-3224普通平衡树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;

const int N = 100010;

struct node {
    int l, r, val;
    int h, sz;  
};

node tree[N];
int cnt, root, n;

inline void newnode(int &now, int val)
{
    now = ++cnt;
    tree[now].val = val;
    tree[now].sz = 1;
}

inline void update(int now)
{
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + 1;
    tree[now].h = max(tree[tree[now].l].h, tree[tree[now].r].h) + 1;
}

inline int calc(int now)
{
    return tree[tree[now].l].h - tree[tree[now].r].h;
}

inline void zag(int &now)
{
    int r = tree[now].r;
    tree[now].r = tree[r].l;
    tree[r].l = now;
    now = r;
    update(tree[now].l);
    update(now);
}

inline void zig(int &now)
{
    int l = tree[now].l;
    tree[now].l = tree[l].r;
    tree[l].r = now;
    now = l;
    update(tree[now].r);
    update(now);
}

inline void check(int &now)
{
    int nf = calc(now);
    if (nf > 1) {
        int lf = calc(tree[now].l);
        if (lf > 0) zig(now);
        else {
            zag(tree[now].l);
            zig(now);
        }
    }
    else if (nf < -1) {
        int rf = calc(tree[now].r);
        if (rf < 0) zag(now);
        else {
            zig(tree[now].r);
            zag(now);
        }
    }
    else if (now) update(now);
}

void insert(int &now, int val)
{
    if (0 == now) newnode(now, val);
    else if (val < tree[now].val) insert(tree[now].l, val);
    else insert(tree[now].r, val);
    check(now);
}

int find(int &now, int fa)
{
    int res = 0;
    if (0 == tree[now].l) {
        res = now;
        tree[fa].l = tree[now].r;
    }
    else {
        res = find(tree[now].l, now);
        check(now);
    }
    return res;
}

void del(int &now, int val)
{
    if (val == tree[now].val) {
        int l = tree[now].l, r = tree[now].r;
        if (0 == l || 0 == r) now = l + r;
        else {
            now = find(r, r);
            if (now != r) tree[now].r = r;
            tree[now].l = l;
        }
    }
    else if (val < tree[now].val) del(tree[now].l, val);
    else del(tree[now].r, val);
    check(now);
}

int qrank(int val)
{
    int now = root, rank = 1;
    while (now) {
        if (val <= tree[now].val) now = tree[now].l;
        else {
            rank = rank + tree[tree[now].l].sz + 1;
            now = tree[now].r;
        }
    }
    return rank;
}

int qnum(int rank)
{
    int now = root;
    while (now) {
        if (tree[tree[now].l].sz + 1 == rank) break;
        else if (tree[tree[now].l].sz >= rank) now = tree[now].l;
        else {
            rank = rank - tree[tree[now].l].sz - 1;
            now = tree[now].r;
        }
    }
    return tree[now].val;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int op, x;
        scanf("%d%d", &op, &x);
        if (1 == op) insert(root, x);
        else if (2 == op) del(root, x);
        else if (3 == op) printf("%d\n", qrank(x));
        else if (4 == op) printf("%d\n", qnum(x));
        else if (5 == op) printf("%d\n", qnum(qrank(x) - 1));
        else printf("%d\n", qnum(qrank(x + 1)));
    }
    return 0;
}

Splay

在Splay上一系列操作都基于伸展操作，伸展操作能够让出现频率(包括查询，插入，删除)较高的元素能够更靠近根节点，从而使查询、插入、删除整体的时间的变少

1
2
3
4
5
6
struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int sz;     // 以该节点为根的子树大小
    int cnt;    // 数据出现的次数
};

Splay在每次操作后，一般把节点伸展到根节点处，而伸展操作又是通过左旋和右旋来实现的，分为以下六种情况，每种情况都是将x节点伸展到根节点处

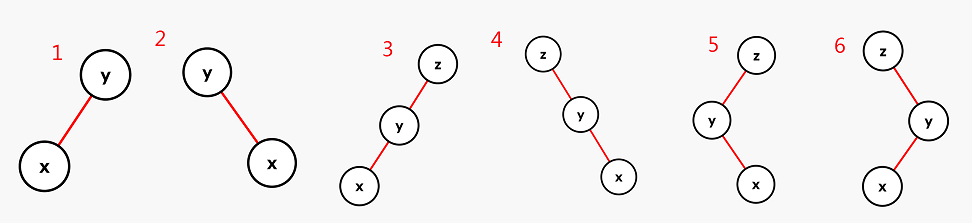
情况1：对y右旋就可以将x节点伸展到根节点处，称为zig

情况2：对y左旋就可以将x节点伸展到根节点处，称为zag

情况3：先对节点z右旋，再对节点y右旋即可，称为zig-zig

情况4：与情况3相反，先对节点左旋，再对节点y左旋即可，称为zag-zag

情况5：先左旋节点y，再右旋节点z即可，称为zag-zig

情况6：与情况5相反，先右旋节点y，再左旋节点z，称为zig-zag

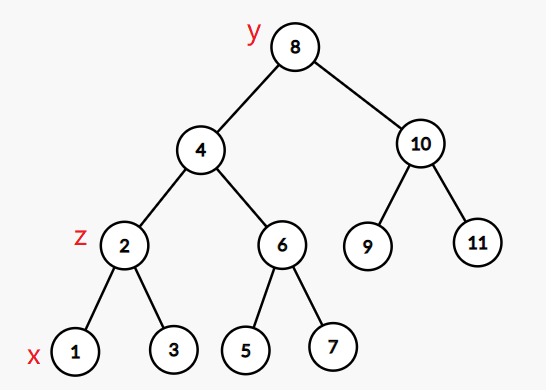
如果需要将x节点伸展到y节点处，我们只需要递归把x节点伸展到z节点处，然后按照情况3处理即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void splaying(int x, int &y)
{
    if (x == y) return;
    int &l = spl[y].l, &r = spl[y].r;
    if (x == l) zig(y);
    else if (x == r) zag(y);
    else {
        if (spl[x].val < spl[y].val) {
            if(spl[x].val < spl[l].val) {
                splaying(x, spl[l].l);
                zig(y), zig(y);
            }
            else {
                splaying(x, spl[l].r);
                zag(l), zig(y);
            }
        }
        else {
            if (spl[x].val > spl[r].val) {
                splaying(x, spl[r].r);
                zag(y), zag(y);
            }
            else {
                splaying(x, spl[r].l);
                zig(r), zag(y);
            }
        }
    }
}

注意：zig、zag函数的参数是引用传递，旋转后节点会发生改变，所以情况3执行的是zig(y)，zig(y)，splaying函数递归的出口是情况1和情况2

splay的插入操作和二叉树的插入操作差不多，插入后，将新插入的节点旋转到根节点即可

对于删除操作，splay则是先把需要删除的节点now伸展到根节点，找到节点now的后继节点，将后继节点伸展为根节点的右儿子，显然被伸展过的后继节点没有左儿子，此时我们只需要将后继节点的左儿子指向根节点的左儿子，将根节点指向这个后继节点即可，删除后需要更新根节点的sz

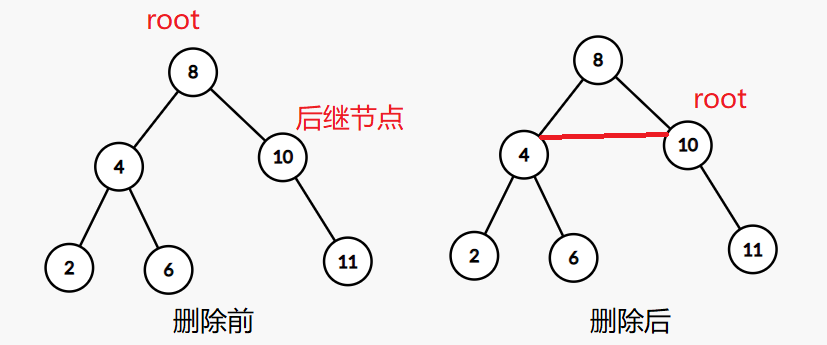
查询某个数的排名qrank(x)和查询某个排名上的数qnum(x)和替罪羊树差不多，只是在查询之后，需要将查询到的节点伸展到根节点

例题：bzoj-3224普通平衡树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;

const int N = 100010;

struct node {
    int l, r, val;
    int sz, cnt;
};

node spl[N];
int cnt, root, n;

inline void newnode(int &now, int val)
{
    now = ++cnt;
    spl[now].val = val;
    spl[now].sz++;
    spl[now].cnt++;
}

inline void update(int now)
{
    spl[now].sz = spl[spl[now].l].sz + spl[spl[now].r].sz + spl[now].cnt;
}

inline void zig(int &now)
{
    int l = spl[now].l;
    spl[now].l = spl[l].r;
    spl[l].r = now;
    now = l;
    update(spl[now].r);
    update(now);
}
inline void zag(int &now)
{
    int r = spl[now].r;
    spl[now].r = spl[r].l;
    spl[r].l = now;
    now = r;
    update(spl[now].l);
    update(now);
}

void splaying(int x, int &y)
{
    if (x == y) return;
    int &l = spl[y].l, &r = spl[y].r;
    if (x == l) zig(y);
    else if (x == r) zag(y);
    else {
        if (spl[x].val < spl[y].val) {
            if(spl[x].val < spl[l].val) {
                splaying(x, spl[l].l);
                zig(y), zig(y);
            }
            else {
                splaying(x, spl[l].r);
                zag(l), zig(y);
            }
        }
        else {
            if (spl[x].val > spl[r].val) {
                splaying(x, spl[r].r);
                zag(y), zag(y);
            }
            else {
                splaying(x, spl[r].l);
                zig(r), zag(y);
            }
        }
    }
}

inline void delnode(int now)
{
    splaying(now, root);
    if (spl[now].cnt > 1) {
        spl[now].sz--;
        spl[now].cnt--;
    }
    else if (spl[root].r) {
        int p = spl[root].r;
        while (spl[p].l) p = spl[p].l;
        splaying(p, spl[root].r);
        spl[spl[root].r].l = spl[root].l;
        root = spl[root].r;
        update(root);
    }
    else root = spl[root].l;
}

void insert(int &now, int val)
{
    if (0 == now) {
        newnode(now, val);
        splaying(now, root);
    }
    else if (val < spl[now].val) insert(spl[now].l, val);
    else if (val > spl[now].val) insert(spl[now].r, val);
    else {
        spl[now].sz++;
        spl[now].cnt++;
        splaying(now, root);
    }
}

void del(int now, int &val)
{
    if (spl[now].val == val) delnode(now);
    else if (val < spl[now].val) del(spl[now].l, val);
    else del(spl[now].r, val);
}

int qrank(int val)
{
    int now = root, rank = 1;
    while (now) {
        if (spl[now].val == val) {
            rank += spl[spl[now].l].sz;
            splaying(now, root);
            break;
        }
        if (val <= spl[now].val) now = spl[now].l;
        else {
            rank = rank + spl[spl[now].l].sz + spl[now].cnt;
            now = spl[now].r;
        }
    }
    return rank;
}

int qnum(int rank)
{
    int now = root;
    while (now) {
        int lz = spl[spl[now].l].sz;
        if (lz + 1 <= rank && rank <= lz + spl[now].cnt) {
            splaying(now, root);
            break;
        }
        else if (lz >= rank) now = spl[now].l;
        else {
            rank = rank - lz - spl[now].cnt;
            now = spl[now].r;
        }
    }
    return spl[now].val;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int op, x;
        scanf("%d%d", &op, &x);
        if (1 == op) insert(root, x);
        else if (2 == op) del(root, x);
        else if (3 == op) printf("%d\n", qrank(x));
        else if (4 == op) printf("%d\n", qnum(x));
        else if (5 == op) printf("%d\n", qnum(qrank(x) - 1));
        else printf("%d\n", qnum(qrank(x + 1)));
    }
    return 0;
}

splay也能像fhq-Treap一样能够对区间进行操作，同样按照元素在序列中的下标来维护二叉树的性质，当对区间[l,r]操作时，可以先将下标为l-1的节点伸展到根节点，将下标为r+1的节点伸展为根节点的右儿子，根据二叉搜索树的性质，显然根节点右儿子的左子树表示的区间就是[l,r]，我们就可以像fhq-Treap、线段树一样用懒标记解决区间问题

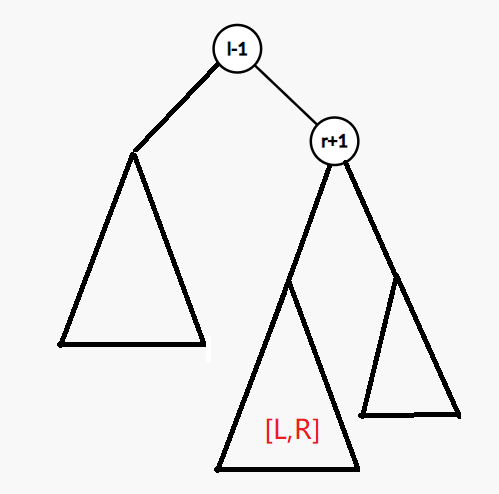
当需要在下标为x的元素后面插入一个新的元素时，我们可以先把下标为x的节点伸展到根节点，再将下标为x+1的节点伸展为根节点的右儿子，根据二叉树的性质，此时根节点右儿子的左子树为空，所以将这个新节点变为根节点右儿子的左子树即可

当需要删除下标为x的元素时，可以先把下标为x-1的节点伸展到根节点，再将下标为x+1的节点伸展为根节点的右儿子，根据二叉树的性质有，根节点右儿子的左子树就是我们需要删除的那个元素，直接将根节点右儿子的左子树变为空即可

注意：对于splay区间操作，一般在序列前后各加一个哨兵，方便处理，但由于在序列开始加入了哨兵，当处理序列上的区间[l,r]时，在splay上的区间应该是[l+1,r+1]

例题：bzoj-3223 文艺平衡树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>

using namespace std;

const int N = 100010;

struct node {
    int fa, sz, ch[2], rev;
};

node spl[N];
int n, cnt, root, m;
vector<int> v;

inline int ident(int x)
{
    return spl[spl[x].fa].ch[1] == x;
}

inline void connect(int x, int fa, int k)
{
    spl[fa].ch[k] = x;
    spl[x].fa = fa;
}

inline void update(int x)
{
    spl[x].sz = spl[spl[x].ch[0]].sz + spl[spl[x].ch[1]].sz + 1;
}

inline void pushdown(int x)
{
    if (0 == spl[x].rev) return;
    swap(spl[x].ch[0], spl[x].ch[1]);
    spl[spl[x].ch[0]].rev ^= 1;
    spl[spl[x].ch[1]].rev ^= 1;
    spl[x].rev = 0;
};

void rotate(int x)
{
    int f = spl[x].fa, ff = spl[f].fa, k = ident(x);
    connect(spl[x].ch[k ^ 1], f, k);
    connect(x, ff, ident(f));
    connect(f, x, k ^ 1);
    update(f);
    update(x);
}

inline void splaying(int x, int t)
{
    if (0 == t) root = x;
    while (spl[x].fa != t) {
        int f = spl[x].fa, ff = spl[f].fa;
        if (ff != t) {
            if (ident(f) == ident(x)) rotate(f);
            else rotate(x);
        }
        rotate(x);
    }
}

inline int find(int x)
{
    int now = root;
    x--;
    pushdown(now);
    while (x != spl[spl[now].ch[0]].sz) {
        if (spl[spl[now].ch[0]].sz < x) {
            x = x - spl[spl[now].ch[0]].sz - 1;
            now = spl[now].ch[1];
        }
        else now = spl[now].ch[0];
        pushdown(now);
    }
    return now;
}

int build(int l, int r)
{
    if (l > r) return 0;
    int mid = (l + r) / 2;
    connect(build(l, mid - 1), mid, 0);
    connect(build(mid + 1, r), mid, 1);
    spl[mid].rev = 0;
    update(mid);
    return mid;
}

void dfs(int now)
{
    if (0 == now) return;
    pushdown(now);
    dfs(spl[now].ch[0]);
    v.push_back(now);
    dfs(spl[now].ch[1]);
}

int main()
{
    scanf("%d%d", &n, &m);
    root = build(1, n + 2);
    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        int L = find(l), R = find(r + 2);
        splaying(L, 0);
        splaying(R, root);
        spl[spl[R].ch[0]].rev ^= 1;
    }
    dfs(root);
    for (int i = 1; i < (int)v.size() - 1; i++) {
        printf("%d", v[i] - 1);
        printf(i == (int)v.size() - 2 ? "\n" : " ");
    }
    return 0;
}

例题：poj-3580 SuperMemo

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;

const int N = 200010;
const int M = 20;
const int INF = 0x3f3f3f3f;

struct node {
    int ch[2], fa, sz;
    int val, imin, rev, lz;
};

node spl[N];
int n, m, cnt, root, a[N];

inline void clear(int x)
{
    spl[x].ch[0] = spl[x].ch[1] = 0;
    spl[x].fa = spl[x].sz = spl[x].val = 0;
    spl[x].imin = spl[x].rev = spl[x].lz = 0;
}

inline int newnode(int val)
{
    spl[++cnt].sz = 1;
    spl[cnt].val = val;
    spl[cnt].imin = val;
    return cnt;
}

inline int ident(int x)
{
    return spl[spl[x].fa].ch[1] == x;
}

inline void update(int x)
{
    spl[x].sz = spl[spl[x].ch[0]].sz + spl[spl[x].ch[1]].sz + 1;
    spl[x].imin = spl[x].val;
    if (spl[x].ch[0]) spl[x].imin = min(spl[x].imin, spl[spl[x].ch[0]].imin);
    if (spl[x].ch[1]) spl[x].imin = min(spl[x].imin, spl[spl[x].ch[1]].imin);
}

inline void connect(int x, int fa, int k)
{
    spl[fa].ch[k] = x;
    spl[x].fa = fa;
}

inline void flip(int x)
{
    spl[spl[x].ch[0]].rev ^= 1;
    spl[spl[x].ch[1]].rev ^= 1;
    swap(spl[x].ch[0], spl[x].ch[1]);
    spl[x].rev = 0;
}

inline void add(int x, int val)
{
    spl[x].val += val;
    spl[x].imin += val;
    spl[x].lz += val;
}

inline void pushdown(int x)
{
    if (0 == x) return;
    if (spl[x].rev) flip(x);
    if (spl[x].lz) {
        add(spl[x].ch[0], spl[x].lz);
        add(spl[x].ch[1], spl[x].lz);
        spl[x].lz = 0;
    }
}

int build(int l, int r, int fa)
{
    if (l > r) return 0;
    int mid = (l + r) >> 1, now = ++cnt;
    spl[now].fa = fa;
    spl[now].val = a[mid];
    spl[now].ch[0] = build(l, mid - 1, now);
    spl[now].ch[1] = build(mid + 1, r, now);
    update(now);
    return now;
}

int find(int x)
{
    int now = root;
    while (now) {
        pushdown(now);
        if (x <= spl[spl[now].ch[0]].sz) now = spl[now].ch[0];
        else {
            x = x - spl[spl[now].ch[0]].sz - 1;
            if (0 == x) break;
            now = spl[now].ch[1];
        }
    }
    return now;
}

void rotate(int x)
{
    int f = spl[x].fa, ff = spl[f].fa, k = ident(x);
    pushdown(f);
    pushdown(x);
    connect(spl[x].ch[k ^ 1], f, k);
    connect(x, ff, ident(f));
    connect(f, x, k ^ 1);
    update(f);
    update(x);
}

void splaying(int x, int t)
{
    if (0 == t) root = x;
    while (spl[x].fa != t) {
        int f = spl[x].fa, ff = spl[f].fa;
        if (ff != t) {
            if (ident(f) == ident(x)) rotate(f);
            else rotate(x);
        }
        rotate(x);
    }
}

void qadd(int l, int r, int d)
{
    int ql = find(l), qr = find(r + 2);
    splaying(ql, 0);
    splaying(qr, root);
    spl[spl[spl[root].ch[1]].ch[0]].imin += d;
    spl[spl[spl[root].ch[1]].ch[0]].val += d;
    spl[spl[spl[root].ch[1]].ch[0]].lz += d;
    update(spl[root].ch[1]);
    update(root);
}

void qreverse(int l, int r)
{
    if (l == r) return;
    int ql = find(l), qr = find(r + 2);
    splaying(ql, 0);
    splaying(qr, root);
    spl[spl[spl[root].ch[1]].ch[0]].rev ^= 1;
}

void qrevolve(int l, int r, int d)
{
    d %= (r - l + 1);
    if (0 == d) return;
    int ql = find(r - d + 1), qr = find(r + 2);
    splaying(ql, 0);
    splaying(qr, root);
    int now = spl[spl[root].ch[1]].ch[0];
    spl[spl[root].ch[1]].ch[0] = 0;
    update(spl[root].ch[1]);
    update(root);
    ql = find(l), qr = find(l + 1);
    splaying(ql, 0);
    splaying(qr, root);
    connect(now, spl[root].ch[1], 0);
    update(spl[root].ch[1]);
    update(root);
}

void qinsert(int x, int d)
{
    int ql = find(x + 1), qr = find(x + 2);
    splaying(ql, 0);
    splaying(qr, root);
    connect(newnode(d), spl[root].ch[1], 0);
    update(spl[root].ch[1]);
    update(root);
}

void qdel(int x)
{
    int ql = find(x), qr = find(x + 2);
    splaying(ql, 0);
    splaying(qr, root);
    int del = spl[spl[root].ch[1]].ch[0];
    clear(del);
    spl[spl[root].ch[1]].ch[0] = 0;
    update(spl[root].ch[1]);
    update(root);
}

int qimin(int l, int r)
{
    int ql = find(l), qr = find(r + 2);
    splaying(ql, 0);
    splaying(qr, root);
    return spl[spl[spl[root].ch[1]].ch[0]].imin;
}

int main()
{
    scanf("%d", &n);
    for (int i = 2; i <= n + 1; i++) scanf("%d", &a[i]);
    a[1] = -INF, a[n + 2] = INF;
    root = build(1, n + 2, 0);
    scanf("%d", &m);
    while (m--) {
        char s[M];
        int x, y, d;
        scanf("%s", s + 1);
        if ('A' == s[1]) {
            scanf("%d%d%d", &x, &y, &d);
            qadd(x, y, d);
        }
        else if ('R' == s[1] && 'E' == s[4]) {
            scanf("%d%d", &x, &y);
            qreverse(x, y);
        }
        else if ('R' == s[1] && 'O' == s[4]) {
            scanf("%d%d%d", &x, &y, &d);
            qrevolve(x, y, d);
        }
        else if ('I' == s[1]) {
            scanf("%d%d", &x, &d);
            qinsert(x, d);
        }
        else if ('D' == s[1]) {
            scanf("%d", &x);
            qdel(x);
        }
        else {
            scanf("%d%d", &x, &y);
            printf("%d\n", qimin(x, y));
        }
    }
    return 0;
}

练习：

  1. bzoj - 1503 [NOI2004]郁闷的出纳员

  2. luogu - 3850 [TJOI2007]书架

  3. luogu - 2286 [HNOI2004]宠物收养场

  4. bzoj - 1588 [HNOI2002]营业额统计